Understanding Sampling rate, point rate, and resolution of AWGs

This article provides a description about one way some arbitrary waveform generators (AWGs) behave and how to determine and use the function to create arbitrary waveforms.  There are generally two different types of AWGs in the current market today, some of which are AWGs based on using a DDS (direct digital synthesis) architecture while some are what's considered a true AWG.  In this article, we will describe one method of how an AWG based on a DDS type architecture behave and how to determine points, sampling rate, and resolution.

In general, AWGs follow a formula in calculating and creating the arbitrary waveform based on a relationship between number of points, frequency, and point rate.  It is as follows:

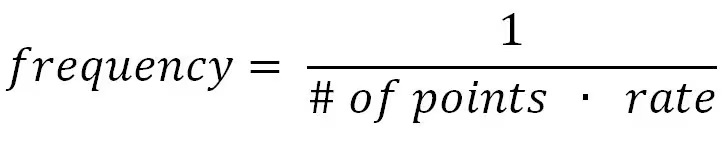
Depending on how many points are defined in the arbitrary memory, the frequency and point rate are directly affected.  Note:  Point rate is the reciprocal of the sampling rate.  For example, sampling rate of 100 MSa/s is equivalent to point rate of 10 ns.

If number of points increase, frequency will decrease also if rate is to stay the same.  Likewise, changing the waveform frequency (or period) will affect the point rate unless points defined in the arbitrary memory are adjusted.  Another way to visualize this formula is to look at the graph below:

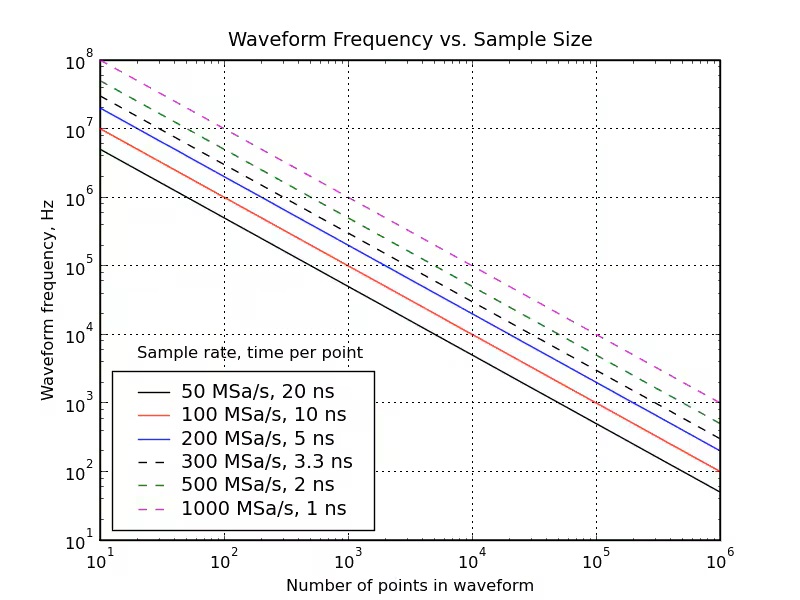
Take for example, you want to create an arbitrary waveform using 50000 points and output at a frequency of 1 kHz.  Depending on the limitations of the AWG, the point rate will be 20 ns per point.  Or, equivalent to 50MSa/s.  However, if the waveform used 120000 points instead and the AWG has a limitation of 100 MSa/s, the frequency of the waveform will be limited as the point rate will be fixed at the sampling rate, which is equivalent to 10 ns per point.  In which case, frequency will be limited to 833.3 Hz instead of 1 kHz.

Not all AWGs behave in this fashion.  Some AWGs, to maintain a certain sampling rate, will oversample or skip some points in the arbitrary memory rather than control and adjust the frequency.

In terms of amplitude, in general AWGs will follow the formula below based on the bit resolution.  Below is the formula used to calculate amplitude based on points in arbitrary memory for an AWG with 14-bit vertical resolution.

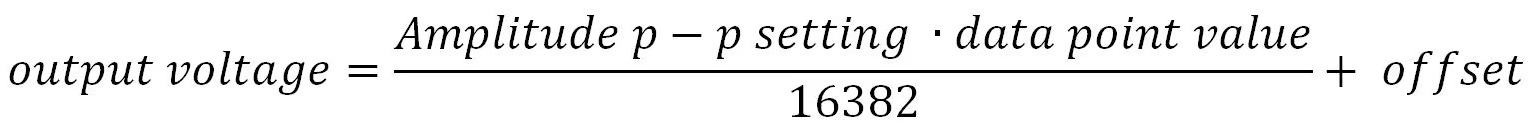
Here, 16382 are the total number of available data values that can be defined for amplitude, which is based on vertical resolution (14-bit).  If the AWG has different vertical bit resolution defined, than the total number of available data will need to be changed in the formula.  The amplitude p-p setting is the peak to peak setting on the AWG.  Most AWGs will have this setting available to control the amplitude of the arbitrary waveform.  By inputting that value into the formula and defining the data point values drawn or set in arbitrary memory, the actual output voltage amplitude can be determined from the formula.  In this example, data point value ranges anywhere between -8191 to 8191 as these range of numbers equate to total number of available data values, 16382.